Classification of sentences of a semantical system
- Title
- Classification of sentences of a semantical system
- Description
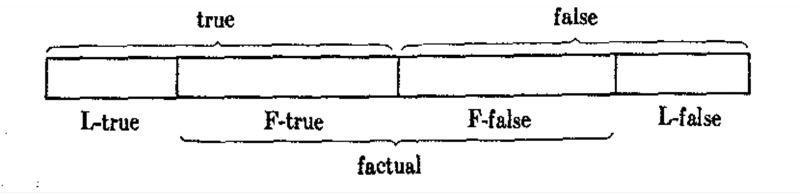
- We call a sentence of a semantical system S (logically true or) L-true if it is true in such a way that the semantical rules of S suffice for establishing its truth. We call a sentence (logically false or) L -false if it is false in such a way that the semantical rules suffice for finding that it is false. The two terms just defined and all other terms defined on their basis we call L-semantical terms. If a sentence is either L-true or L-false, it is called L-determinate, otherwise (L-indeterminate or) factual. (The terms ‘L-true’, ‘L-false’, and ‘factual’ correspond to the terms ‘analytic’, ‘contradictory’, and ‘synthetic’, as they are used in traditional terminology, usually without exact definitions.) If a factual sentence is true, it is called (factually true or) F-true; if it is false, (factually false or) F -false. Every sentence which contains only logical signs is L-determinate. This is one of the chief characteristics distinguishing logical from descriptive signs. (Example: ‘For every object x and every property F, if x is an F then x is an F’ is L-true.)
- Creator
- Carnap, Rudolf
- Date
- 1939
- Bibliographic Citation
- Carnap, Rudolf. 1939. Foundations of Logic and Mathematics. International Encyclopedia of Unified Science. Volume 1, Number 3. Tenth Impression 1963. The University of Chicago Press. Page 13.
New Tags
Part of Classification of sentences of a semantical system