An interpreted system of physics
Item
-
Title
-
An interpreted system of physics
-
Description
-
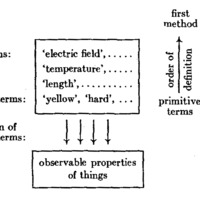
Suppose we have in mind the following purpose for our syntactical and semantical description of the system of physics: the description of the system shall teach a layman to understand it, i.e., to enable him to apply it to his observations in order to arrive at explanations and predictions. A layman is meant as one who does not know physics but has normal senses and understands a language in which observable properties of things can be described (e.g., a suitable part of everyday nonscientific English). A rule like ‘the sign ‘P’ designates the property of being blue’ will do for the purpose indicated; but a rule like ‘the sign ‘Q’ designates the property of being electrically charged’ will not do. In order to fulfill the purpose, we have to give semantical rules for elementary terms only, connecting them with observable properties of things. For our further discussion we suppose the system to consist of rules of this kind, as indicated in the … diagram.
Now let us go back to the construction of the calculus. We have first to decide at which end of the series of terms to start the construction. Should we take elementary terms as primitive signs, or abstract terms? … The first method consists in taking elementary terms as primitive and then introducing on their basis further terms step by step, up to those of highest abstraction. … The first method has the advantage of exhibiting clearly the connection between the system and observation and of making it easier to examine whether and how a given term is empirically founded. …
If, on the other hand, abstract terms are taken as primitive—according to the second method, the one used in scientific physics—then the semantical rules have no direct relation to the primitive terms of the system but refer to terms introduced by long chains of definitions. The calculus is first constructed floating in the air, so to speak; the construction begins at the top and then adds lower and lower levels. Finally, by the semantical rules, the lowest level is anchored at the solid ground of the observable facts.
-
Creator
-
Carnap, Rudolf
-
Date
-
1939
-
Source
-
Foundations of Logic and Mathematics
-
Bibliographic Citation
-
Carnap, Rudolf. 1939. Foundations of Logic and Mathematics. International Encyclopedia of Unified Science. Volume 1, Number 3. Tenth Impression 1963. The University of Chicago Press. Pages 62-65.