Classification of sentences of a semantical system

Title: Classification of sentences of a semantical system
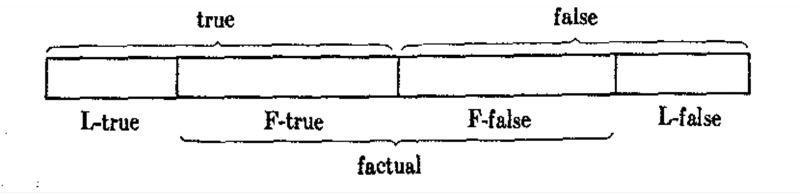
Description: We call a sentence of a semantical system S (logically true or) L-true if it is true in such a way that the semantical rules of S suffice for establishing its truth. We call a sentence (logically false or) L -false if it is false in such a way that the semantical rules suffice for finding that it is false. The two terms just defined and all other terms defined on their basis we call L-semantical terms. If a sentence is either L-true or L-false, it is called L-determinate, otherwise (L-indeterminate or) factual. (The terms ‘L-true’, ‘L-false’, and ‘factual’ correspond to the terms ‘analytic’, ‘contradictory’, and ‘synthetic’, as they are used in traditional terminology, usually without exact definitions.) If a factual sentence is true, it is called (factually true or) F-true; if it is false, (factually false or) F -false. Every sentence which contains only logical signs is L-determinate. This is one of the chief characteristics distinguishing logical from descriptive signs. (Example: ‘For every object x and every property F, if x is an F then x is an F’ is L-true.)
Creator: Carnap, Rudolf
Date: 1939
Source: Foundations of Logic and Mathematics
Bibliographic Citation: Carnap, Rudolf. 1939. Foundations of Logic and Mathematics. International Encyclopedia of Unified Science. Volume 1, Number 3. Tenth Impression 1963. The University of Chicago Press. Page 13.